Putting collation of text witnesses on a formal basis

Abstract of the paper

Details on the Experiments

We compared TSaligner with CollateX on different texts. CollateX provides two collation algorithms (and a third experimental one) to choose from, the Dekker-algorithm and the Needle-Wunsch-algorithm. Because CollateX's distance measures are designed for sentence word alignment rather than paragraph alignment, we have added two new distance measures to CollateX, the normalized Levenshtein distance and the Jaccard distance, which are more appropriate for paragraph alignment. We worked with the CollateX version dated June 18 2019 and added our custom distance measures –the latest official builds of CollateX could not be used because they threw different exceptions.

Distance measures

To find pairs of paragraphs that are similar and could be aligned, we need to define when paragraphs form a "good pair" or a "match". This is done by a so-called distance or similarity function. It takes two paragraphs and returns a result indicating how "good" a pair is. Often a threshold is defined and if the distance between the paragraphs is below or equal to the threshold they are considered to "match". Because finding a good measure for the distance of paragraphs is a task on its own, aligners normally provide a set of distance measures or allow to specify a custom distance measure. We choose to test with two distance measures:

The Levenshtein distance is a well known distance function and very useful, e.g., for comparing sentences. In the case of paragraph alignment it is more suitable to normalize the Levenshtein distance by the length of the two paragraphs. If we omit the normalization and define a threshold the result will depend too much on the lengths of the paragraphs. The normalized Levenshtein Distance (nLD) shows the percentage of changed tokens to convert one paragraph to the other.

Short example

t¹_i: "wie das Stroh zu Gold werden sollte"

t²_j: "wie man Stroh zu Gold spinnen konnte"

|t¹_i| = 35

|t²_j| = 36

nLD(t¹_i, t²_j)  =  

levenshtein(t¹_i, t²_j)

max(|t¹_i|, |t²_j|)

  =  

10

36

  ≈   0.278

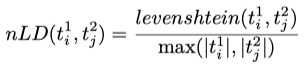
Another distance function we used is the Jaccard Distance (JD). Our experiments show that this distance measure leads to better results when aligning paragraphs than the (normalized) Levenshtein distance. It gives the ratio of the number of common words to the number of all words used in the two paragraphs, or rather 1 minus this ratio.

Short example

t¹_i: "wie das Stroh zu Gold werden sollte"

t²_j: "wie man Stroh zu Gold spinnen konnte"

words(t¹_i) = {wie, das, Stroh, zu, Gold, werden, sollte}

words(t²_j) = {wie, man, Stroh, zu, Gold, spinnen, konnte}

words(t¹_i) ∩ words(t²_j) = {wie, Stroh, zu, Gold}

words(t¹_i) ∪ words(t²_j) = {wie, das, Stroh, zu, Gold, werden, sollte, man, spinnen, konnte}

JD(t¹_i, t²_j)  =  1 -  

| words(t¹_i) ∩ words(t²_j) |

| words(t¹_i) ∪ words(t²_j) |

  =  1 -  

4

10

  = 0.6

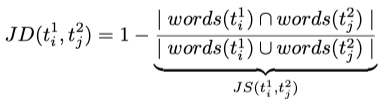
Application of the distance measures in CollateX and TSaligner

CollateX not directly works with distances but it only needs to know whether two paragraphs produce a match or not. Thus, we added a custom distance function for nLD and JD. They produce a match if and only if the calculated distance is below or equal to a given threshold c₃. We tested with values 1.0 and 0.7 for c₃.

TSaligner also uses the distance measures from above but in a slightly more mathematical way. Both distance functions, normalized Levenshtein distance and Jaccard distance, produce results in the interval [0, 1]. We subtract c₃ from the distance. This will partially shift the interval into the negative range, e.g. for c₃ = 0.7 to [-0.7, 0.3]. As not aligning two paragraphs adds a value of 0 to the total distance, we only align paragraphs with distances in the interval [-0.7, 0]. This way we ignore paragraph pairs with distance greater than c₃. For two paragraphs that are aligned, however, their (now negative) distance is included in the costs.

Test data

We compared TSaligner with CollateX on two witnesses of each of the three texts, "Rumpelstilzchen" (in the following we abbreviate it by "Rumpel"), "Wally die Zweifelerin" ("Wally"), and "Aus der Knabenzeit" ("Knab").

The second column indicates the year of origin and the third column the number of paragraphs of the two respective witnesses. The fourth column gives our "rating" of the lengths of the paragraphs in the text witnesses.

Experimental Results

As the assessment of findings in the Humanities is often based on interpretation (cf. [23] in the paper) it is not possible to claim that one alignment is better than another. The assessment usually depends on the humanities question under study. With this in mind, we can only invite the reader to take a closer look at the alignments created by CollateX and TSaligner using the two distance functions, normalized Levenshtein distance and Jaccard distance. Here, we can only reflect our own observations. We believe that these are true for most applications.

When we look at the results of our experiments, TSaligner appears to produce alignments that are better, and by no means worse, than those generated by CollateX:

• Regarding the distance measures, Jaccard distance and normalized Levenshtein-distance don't give many differences when both text witnesses are very similar and TSaligner is used.


• CollateX with normalized Levenshtein distance produces comparably worse results than with Jaccard distance.


• When comparing TSaligner with Jaccard-distance and CollateX with Jaccard-distance, our approach appears to produce better result.

The following three subsections contain the alignments produced by the different approaches. For our internal evaluation the resulting alignments contain an additional column headed by "JS". It gives the Jaccard Similarities of the matched paragraphs which is given by 1 minus the Jaccard distance between the two paragraphs.

We marked the most interesting results for use with a

Downloads

Contact

Martin Luther University Halle-Wittenberg | https://www.informatik.uni-halle.de/ti/mitarbeiter | https://www.informatik.uni-halle.de/ti/

Janis Dähne

Marcus Pöckelmann

Jörg Ritter

Paul Molitor